La domificazione secondo Retorio.


AVENDO in animo di preparare una esposizione esauriente sui sistemi impiegati dagli astrologi ellenistici per suddividere il cielo locale in case, ma non volendo appesantirne il contenuto, qui tratteremo separatamente il sistema di domificazione esposto da Retorio. Il testo, di cui proponiamo la traduzione, si trova in Catalogus codicum astrologorum Graecorum, vol. VIII.1, p. 221. Il capitolo s'intitola Come occorre (procedere per) trovare i gradi (μοιρικῶς) dei centri dei dodici luoghi.[1] Retorio inizia col riferire i dati:[2]

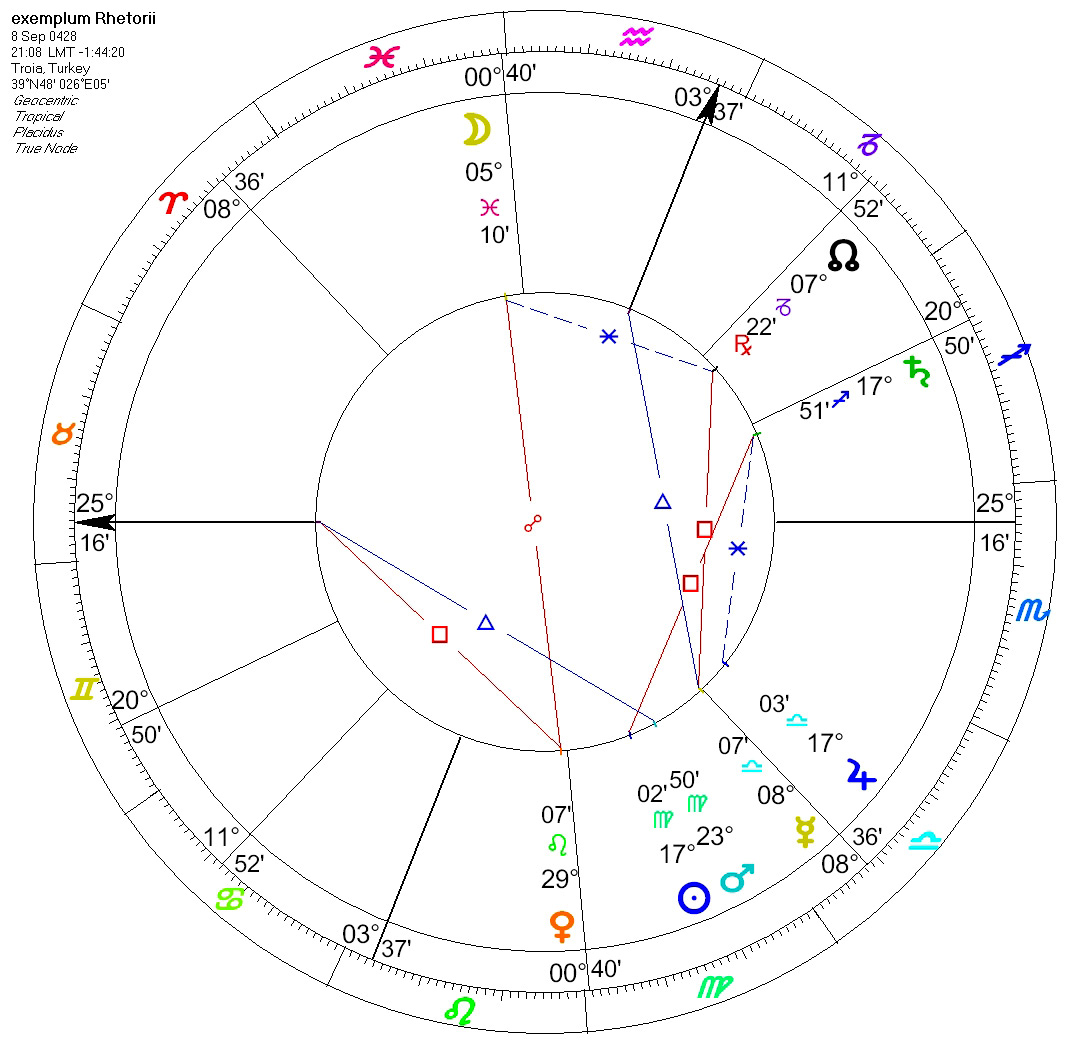
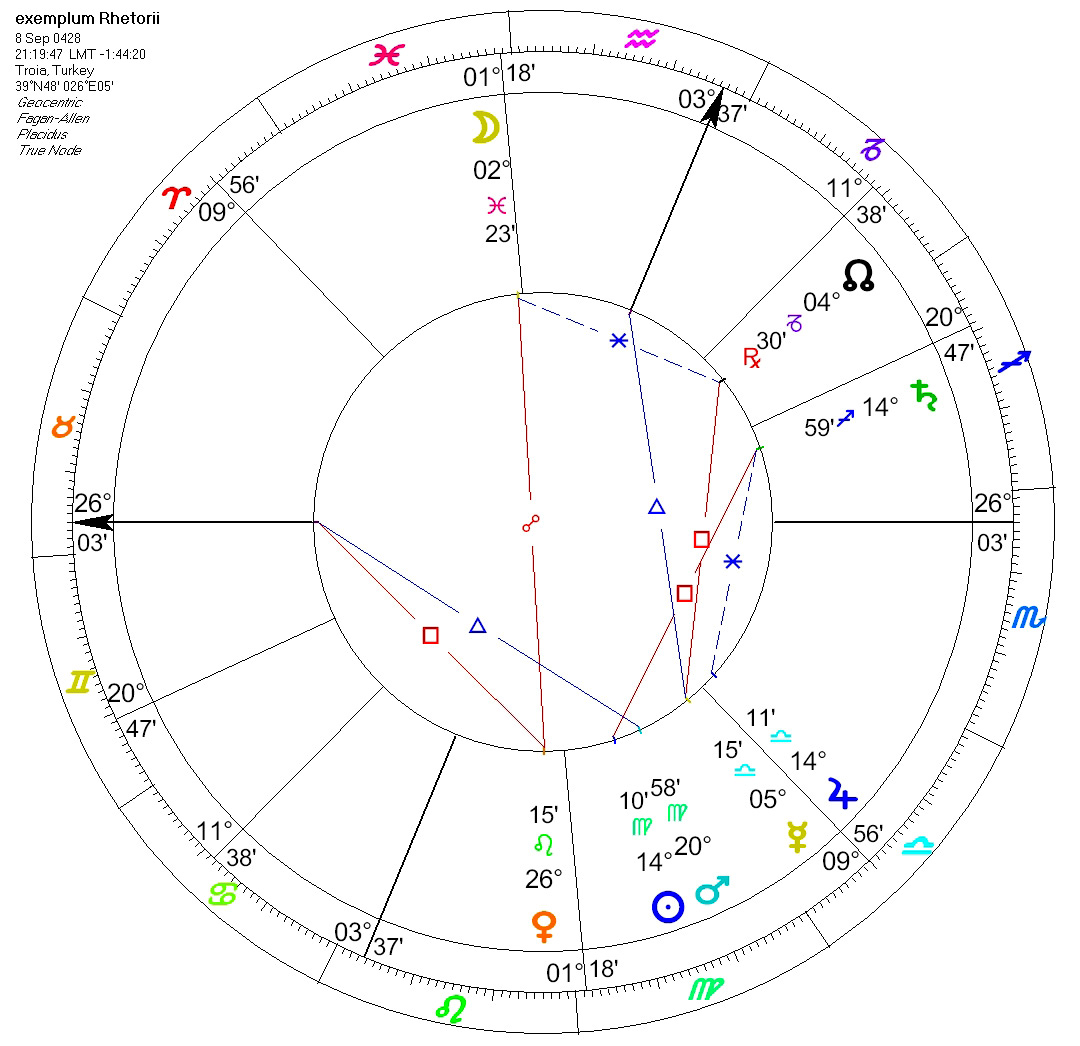
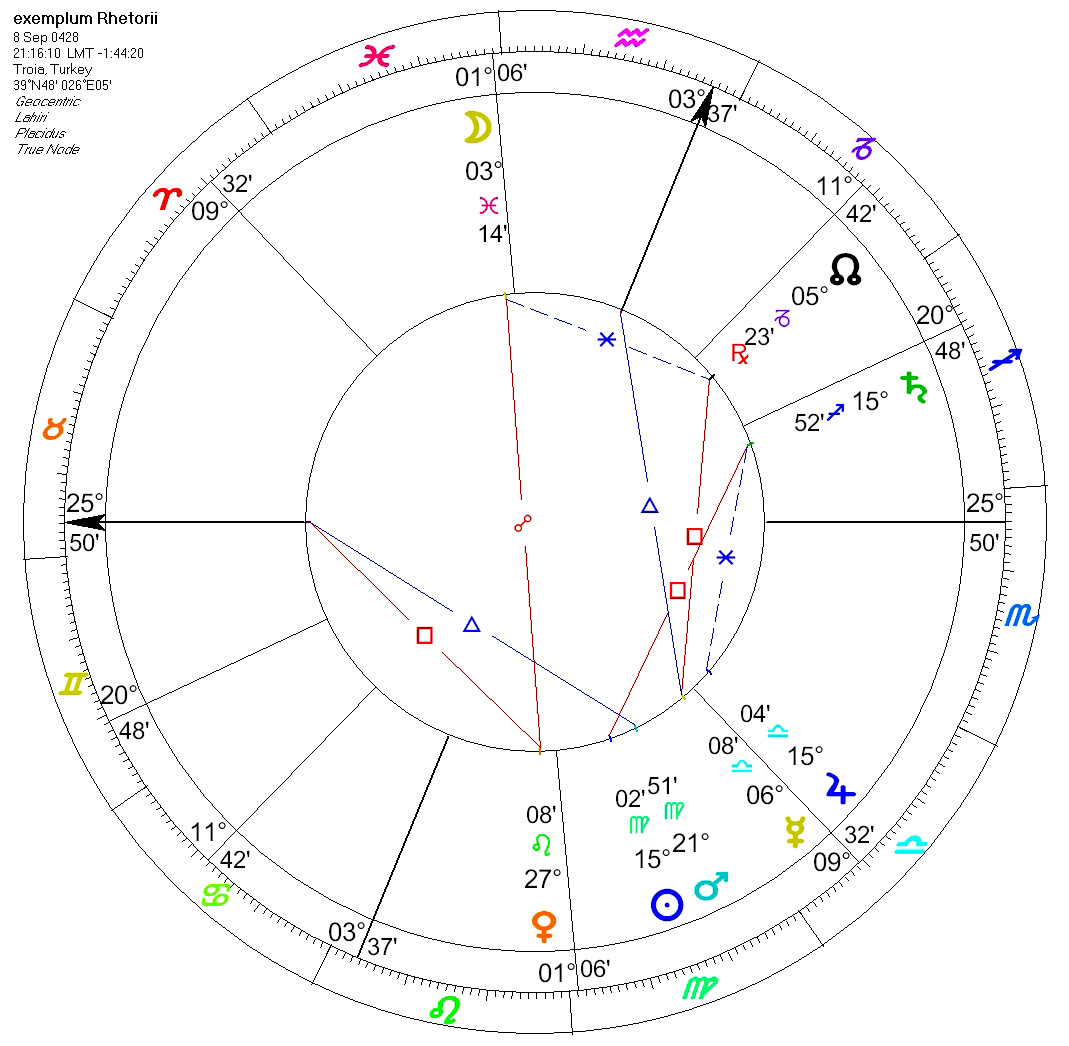
Esempio di genitura: quinto clima, il (giorno) 10 verso l'11 (del mese) di Thoth dell'anno 145 di Diocleziano, inizio della quarta ora della notte; il Sole (si trovava) a 14°19' Vergine, la Luna a 3° 4' Pesci, Saturno a 14°31' Sagittario, Giove a 15°41' Bilancia, Marte a 21°6' Vergine, Venere a 25°40' Leone, Mercurio a 3°37' Bilancia, l'oroscopo a 25° 16' Toro, il medio cielo a 3° 37' Mescitor d'acqua, il nodo lunare a 30°41' Capricorno, il (precedente) sinodo (s'era verificato) a 1°26' Vergine, la (sorte di) Fortuna a 6°31' Sagittario, (quella del) Demone a 14°1' Scorpione.

La data gregoriana è quella dell'8 settembre 428. Per offrire al nostro lettore l'immagine della carta del cielo dell'esempio retoriano, abbiamo impostato in S(olar)F(ire) una località del V° clima, ad es. Troia, in Turchia, con le seguenti coordinate: 39°N48' e 26°E05', alle h. 21h08m, ora locale (LMT): una scelta quasi obbligata, per far coincidere il mediocielo e l'ascendente con quelli dati da Retorio (v. carta in alto, a sinistra). Poi abbiamo richiesto una seconda carta, variando lo zodiaco, da tropico a siderale (Fagan-Allen) (in alto, in centro), ed una terza (in alto, a destra), variando di nuovo lo zodiaco siderale, da Fagan-Allen a Lahiri, in modo che mediocielo e ascendente restassero al loro posto: per lo zodiaco siderale secondo Fagan-Allen abbiamo dovuto modificare l'ora (21h19m47s) e la latitudine (38°N47'), così pure per lo zodiaco secondo Lahiri (21h16m10s e 39°N05'). 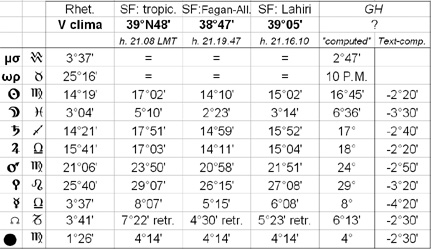Nel prospetto qui a destra, vediamo le differenze: nelle ultime due colonne riportiamo i dati calcolati da GH con i relativi scarti segnalati dagli autori, mentre nella prima colonna, in corrispondenza dei simboli a destra, esponiamo i dati di Retorio, nella seconda quelli dati da SF per lo zodiaco tropico, nella terza quelli secondo lo zodiaco siderale Fagan-Allen, e nella quarta quelli secondo Lahiri. La domificazione è di Placido. Si noterà subito che tra le posizioni di Retorio e quelle dello zodiaco tropico vi è una notevole discrepanza, che si contrae fino a divenire in alcuni casi trascurabile se il confronto viene fatto con i due zodiaci siderali. Eppure, Retorio dice chiaramente d'aver utilizzato lo zodiaco siderale, non quello tropico. Di qui, vien naturale chiedersi perché mai GH metta a confronto dati non confrontabili. Invero, è noto che O. Neugebauer disprezzasse, da bravo scientista qual era,[3] l'astrologia; tuttavia viene il sospetto che sia lui che il suo collega van Hoesen non avessero capito il testo (v. infra). Va da sé che nel seguito le operazioni eseguite da Retorio saranno controllate utilizzando la latitudine di 40°N56' per il V clima e 23°51'20” per l'inclinazione dell'eclittica, entrambe prese da Tolemeo. Riprendiamo la lettura:

Spiegheremo (come trovare) i gradi (di ciascuno) dei dodici luoghi al fine di mostrare secondo il calcolo naturale e logico le distanze in gradi dei luoghi centrali e declinanti nel modo che segue.
Dacché <si prendono> i 5 gradi che preascendono <l'orizzonte>,[4] come dice Tolemeo, sottraendo questi al grado che sorge dato, troveremo l'origine della centralità[5] dell'oroscopo a 20°16' (Toro); a questi gradi corrispondono, sulla sfera retta, tempi ascensionali pari a 137° 44'. Prendendo i tempi orari di 20°16' Toro nel quinto clima, cioè 17° 44',[6] e raddoppiandoli, otterremo tempi orari pari a 35°28', sottratti i quali a 137°44' troveremo una rimanenza di 102°16'; (ebbene,) insieme con questi 102°16' culminano nella sfera retta 13°21' Ariete. <E questi gradi saranno l'inizio della XII casa>.[7]

Dobbiamo soffermarci, per spiegare che cosa siano le ascensioni sulla sfera retta. Tolemeo ne parla nell'ultimo capitolo del libro I dell'Almagesto (p. 47). Se ruotiamo la sfera locale fino a far coincidere l'equatore con un meridiano qualsiasi, noi otterremo la sfera retta, così definita perché equatore ed orizzonte, che in tal caso passa per i poli, si tagliano ad angolo retto e la latitudine dell'osservatore è 0°. In dette condizioni un qualunque segmento dell'eclittica sorgerà all'orizzonte esattamente negli stessi tempi del segmento di ascensione retta (α) corrispondente. Se, ad es., prendiamo sull'eclittica i 30° dell'Ariete, sulla sfera retta essi ascenderanno negli stessi tempi corrispondenti all'ascensione retta dei primi 30° dell'eclittica.[8] Procedendo per mezzo della formula al calcolo dell'α di 30° Ariete, otterremo 27°50', che sono gli stessi tempi ascensionali indicati da Tolemeo. Ma i tempi ascensionali, però, proprio in quanto ascensionali, si presume che sorgano all'orizzonte di un luogo, quale che esso sia.
Teone Alessandrino nel suo Piccolo commentario alle tavole tolemaiche di pronto utilizzo[9] fornisce una Tavola delle ascensioni sulla sfera retta per ogni grado dello zodiaco a qualsiasi latitudine. Detta tavola presuppone che l'osservatore si trovi a mezzogiorno, cioè con il Sole allo zenit, di un luogo qualunque. È noto che il mediocielo (MC) ha sempre latitudine 0° e che l'ascensione obliqua dell'oroscopo è data dall'α del MC + 90°. Se, dunque, all'α di un punto dell'eclittica a mezzogiorno aggiungiamo 90°, otterremo l'ascensione obliqua (αφ) dell'oroscopo.[10] Ma sulla sfera retta non v'è alcuna ascensione obliqua né differenza ascensionale, sicché detta somma darà l'α dell'oroscopo, cui – consultando le tavole – corrisponderà un preciso punto dell'eclittica.
Ebbene, che cosa fa Retorio? Egli ha già trovato il grado ascendente (25°16' Toro), ma, volendo seguire Tolemeo secondo il quale la prima casa inizia cinque gradi prima, toglie 5°: quindi, 25°16' Toro – 5° = 20°16'. Egli cerca, poi, nella Tavola delle ascensioni sulla sfera retta i tempi ascensionali corrispondenti a 20°16' Toro. Qui sotto, proponiamo la tavola calcolata da Excel: i valori in marrone espongono i gradi sessagesimali, quelli sottostanti in nero i corrispondenti decimali. Nella prima colonna sono elencati i gradi dell'eclittica supposti al mediocielo, cioè a mezzogiorno; sulla medesima riga sono date le ascensioni per ogni segno.


Interpolando fra 20° (137°27'51”) e 21° Toro (138°28'39”) troviamo che a 20°16' Toro corrispondono 137°44'(03”), che sono i medesimi tempi ascensionali dati da Retorio.[11] Ora occorre trovare i tempi orari corrispondenti a 20°16' Toro nel V clima. Contrariamente a quanto afferma GH, Teone non dà i tempi orari per ciascun grado, ma solo i tempi ascensionali. Prendiamo quindi la Tavola tolemaica delle ascensioni per il V clima ed, interpolando fra 31°05' (20° Toro) e 38°51' (30° Toro), troveremo che i tempi ascensionali di 20°16' Toro corrispondono a 31°18' (per l'esattezza 31°17'26”). Sottraendo all'α di 20°16' (cioè 47°44'26”) la pseudo-ascensione obliqua (31°18'), otterremo la differenza ascensionale (16°27'); sommando 1/6 di questa diff. asc. a 15°, otterremo i tempi orari di 20°16' Toro, vale a dire 17°44'30”, che Retorio arrotonda a 17°44'.
Siccome ogni casa dista dall'altra 2 ore, Retorio raddoppia l'ora temporale (17°44' × 2) e sottrae 35°28' a 137°44'; quindi riporta il risultato di 102°16' nella Tavola delle ascensioni sulla sfera retta, per trovare a quale grado dell'eclittica corrisponda: egli dice a 13°21' Ariete, anche se in realtà l'interpolazione dà 13°14'(40”), che è il punto dove inizia il XII luogo. Ma procediamo:

E di nuovo nello stesso ordine, sottraendo a 102°16' (i medesimi) 35°28', troveremo una rimanenza di 66°48', con i quali troveremo che insieme culminano, sempre sulla sfera retta, 4°8' Pesci. Saranno per noi proprio questi 4°8' Pesci l'origine dell'undicesimo luogo, [[mentre 3°11' del Mescitor d'acqua (saranno) l'origine del decimo, sicché la Luna viene a trovarsi piuttosto nel decimo luogo]].[12] Ancora, sottraendo 35° 28' ai 66° 48' (avremo) una rimanenza di 31° 20', con i quali troveremo che insieme culminano 29° 7' Capricorno. Saranno proprio questi l'inizio del mediocielo; all'inizio, però, il mediocielo era a 3° 37' Mescitor d'acqua; dunque (l'origine) precede di 4°30'; ma doveva essere di 5°. In effetti differisce di un nulla, di 30'.

Alcune interpolazioni sono poco precise, poiché all'α di (66°48' – 90° =) 336°48' corrispondono sull'eclittica 4°53'(26”). Migliore è quella per la X casa: infatti, insieme con (66°48' – 35°28' =) 31°20', cioè (31°20 – 90° =) 301°20', culminano 29°6'32” Capricorno. Qui Retorio dà una interessante spiegazione del perché si sia verificata una tale pur minima differenza, ma ne riparliamo più sotto.
L'astrologo, poi, prosegue con la suddivisione delle case nel quadrante ad occidente:

Ripetendo i calcoli (πάλιν), dacché da 29°7' Capricorno fino a 29°7' Cancro i tempi delle culminazioni dell'emisfero sono 180°, di cui le simultanee culminazioni da 29°7' Capricorno fino a 20°16' Toro sono sei volte 17° 44', cioè 106° 24',[13] ne consegue che le simultanee culminazioni da 20°16' Toro fino a 29°7' Cancro sono pari ai tempi mancanti al( completamento del)l'emisfero, (ossia) 73°36'.[14] Il terzo di questi è 24°32' tempi. Sottratti i 24°32' ai gradi dati, 31°20', restano 6°48', insieme con i quali culminano 6°13' Capricorno; saranno dunque 6°13' Capricorno l'inizio del IX luogo.[15] Di nuovo, da 6°48' sottratti 24°32', restano 342°16', insieme con i quali culminano 13°42' Sagittario;[16] saranno dunque 13°42' Sagittario l'inizio dell'VIII luogo.[17] Ancora, tolti 24°32' a 342°16', restano 317°44', insieme con i quali culminano 20°16' Scorpione, che è il punto diametrale all'oroscopo. I punti diametrali a questi saranno gli inizi dei luoghi sotterra, cioè il II, III, IV, V, VI.

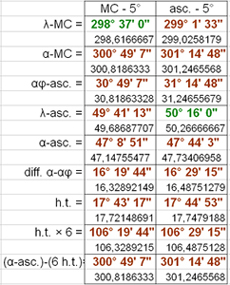E così si conclude il calcolo delle case secondo Retorio. Per trovare ove s'annidi l'errore che ha generato la menzionata discrepanza di 30', rifacciamo i calcoli utilizzando le formule trigonometriche, mantenendo ε = 23° 51' 20” e φ = 40° 56' (V clima). Nel prospetto a sinistra, prima colonna, esponiamo i dati ottenuti partendo dalla longitudine eclittica del MC (in verde); nella seconda colonna i medesimi dati ottenuti partendo dalla longitudine eclittica dell'ascendente. Si noterà che il MC a 28° 37' Capricorno (298°37') pone l'ascendente a 19°41' Toro (49°41'13"), mentre nella seconda colonna l'ascendente a 20°16' Toro (50°16') colloca il MC a 29°02' Capricorno (299°01'33"). In altre parole, questi due dati non possono coesistere. Le ragioni addotte da GH non hanno alcun pregio.[18]. Ma un attento lettore potrebbe chiedere: come mai nelle tre carte del cielo sopra mostrate ascendente e MC corrispondono a quelli dati da Retorio? La risposta è semplice: perché, come più sopra precisato, sono state lievemente modificate sia la latitudine geografica sia l'ora.
Sintetizzando, l'elaborato sistema esposto da Retorio si riduce a poche e semplici operazioni:
1. Trovati l'ascendente e il MC, si detraggono 5° eclittici dall'ascendente;
2. Calcolata l'α dell'ascendente, si computa il suo semiarco, che è poi la distanza in α tra l'ascendente stesso e il MC;
3. Una volta diviso per 3 il semiarco, i corrispondenti punti sull'eclittica saranno l'inizio delle case contenute nel quadrante; e ciascuna sezione di un terzo uguaglia il doppio dell'ora temporal-locale dell'ascendente.
Tale sistema diverrà famoso col nome di “domificazione di Alcabizio” (sec. X), di cui torneremo a parlare in altra sede.[19]
Ora riprendiamo la spiegazione da lui data intorno alla discrepanza di 30', ossia 4°30' anziché 5°:

La causa è questa. Tolemeo dice che né i gradi temporali né quelli locali debbano precedere il centro, bensì quelli dello zodiaco noetico, che non si muove (τοῦ ἀκινήτου) ricalcando i gradi locali e temporali in movimento (τοῦ σχηματίζοντος τὰς κινουμένας τοπικάς τε καὶ χρονικὰς μοίρας). Noi, invece, abbiamo assunto i 5 gradi in movimento e sensibili. Quando, dunque, Tolemeo dice «i (luoghi) esagoni destri a questi 30 gradi (τοὺς ταύταις ταῖς λ΄μοίραις δεξιοὺς ἑξαγώνους)», sta parlando di quelli noetici: sono infatti quelli che si formano l'un l'altro (σχηματίζουσαι ἀλλήλας) ogni 30° con precisione, mentre quelli in movimento si rilevano in modo approssimato.

Va subito rilevato che la citazione è scorretta, poiché Tolemeo dice «i gradi esagoni destri a questi 30 gradi (τὰς ταύταις ταῖς λ΄μοίραις δεξιὰς ἑξαγώνους)». L'uso del maschile (τοὺς) anziché del femminile (τὰς) cambia le carte in tavola e costringe il lettore a pensare ai luoghi invece che ai gradi. È anche possibile che un copista ignorante, leggendo ἑξαγώνους, che vale sia per il maschile che per il femminile, abbia modificato il testo.
Ora confrontiamo la traduzione di GH: «Ptolemy says neither that one must subtract from the center time degrees nor (that one must subtract) longitudinal degrees, but the (degrees) of the ideal and fixed zodiac which (is the basis of the calculation) of the aspects, (i.e.) the variable longitudinal and time degree. We, however, took the variable and perceptible 5 degrees. Thus, when Ptolemy says “and the sextile which is to the right of these 30 degrees,” then he is speaking of the ideal (degrees), for these are (degrees) which always accurately make 30 degrees together; but the variable (degrees) give only an approximate (total).»
In questa traduzione gli autori sembrano aver fatto un po' di confusione.[20] La prima domanda da porsi è: che cos'è questo zodiaco noetico (ὁ νοητὸς ζωδιακός), tradotto da GH con “ideal”?
Un luogo di Origene – citato da Eusebio – cade a fagiolo:[21]

Φέρεται δὴ θεώρημα ἀποδεικνύον τὸν ζωδιακὸν κύκλον ὁμοίως τοῖς πλανωμένοις φέρεσθαι ἀπὸ δυσμῶν ἐπὶ ἀνατολὰς δι ἑκατὸν ἐτῶν μοῖραν μίαν, καὶ τοῦτο τῷ πολλῷ χρόνῳ ἐναλλάττειν τὴν θέσιν τῶν δωδεκατημορίων· ἑτέρου μὲν τυγχάνοντος τοῦ νοητοῦ δωδεκατημορίου, ἑτέρου δὲ τοῦ ὡσανεὶ μορφώματος· τὰ δὲ ἀποτελέσματά φασιν εὑρίσκεσθαι οὐκ ἐκ τοῦ μορφώματος, ἀλλ' ἐκ τοῦ νοητοῦ ζωδίου· ὅπερ οὐ πάνυ τι δυνατὸν καταλαμβάνεσθαι.
È nota la teoria secondo la quale si dimostra che il cerchio zodiacale, come pure gli (astri) erranti, si sposta da occidente verso oriente di un grado ogni cent'anni, e questo fatto col trascorrere del tempo cambia la posizione tra i (rispettivi) dodecatemorii, sicché un dodecatemorio risulta noetico, l'altro (che gli corrisponde) risulta dalla figura. Eppure dicono che gli eventi (a venire) si traggono non dalla figura, ma dal segno noetico. Questo è davvero inconcepibile!

Il cerchio zodiacale che si muove di un grado ogni cent'anni è dunque quello siderale, fatto di figure visibili con gli occhi fisici, mentre l'altro, quello noetico, cioè che si vede con gli occhi della mente,[22] non si muove perché inizia sempre dall'equinozio di primavera, e ricalca quello siderale.[23] L'osservazione più interessante ed astrologicamente preziosa è che gli eventi futuri si traggono – dicono presumibilmente i Caldei – dallo zodiaco tropico, non da quello siderale!
Secondo gli autori di GH «Retorio è sorpreso che...». In realtà, Retorio non manifesta alcuna sorpresa, ma, per salvaguardare la sua professionalità – è solo una nostra ipotesi –, chiama in causa i due zodiaci, quello noetico, cioè tropico, e quello siderale. Che egli abbia utilizzato le posizioni siderali degli astri erranti, l'abbiamo già visto, ma la discrepanza tra il mediocielo di partenza e quello d'arrivo non ha nulla a che vedere con i due zodiaci.
La suddivisione del giorno, dal sorgere al tramonto e dal tramonto al sorgere successivo, in 6 + 6 doppie ore era già nota agli astrologi mesopotamici, cioè ai caldei. Ne era a conoscenza già Erodoto (sec. V): «L'orologio solare, lo gnomone e le dodici parti del giorno, i Greci li appresero dai Babilonesi».[24] In altre parole, la suddivisione del cielo in dodici sezioni di due ore ciascuna era già applicata dai caldei: il nome di tale doppia ora era bēru.[25] Purtroppo, però, l'informazione relativa ai calcoli fu trasmessa in modo vago o impreciso, o non fu trasmessa affatto; il che indusse gli astronomi greci a scervellarsi per trovare una soluzione accettabile.[26]
L'ingegnoso utilizzo delle ascensioni sulla sfera retta presta il fianco, però, a due obiezioni:
1. Ad una qualsivoglia latitudine, che non sia 0°, dacché l'orizzonte non passa più per i poli del mondo, che fine fanno i settori delimitati dai cerchi di declinazione che sulla sfera retta coincidono con i cerchi di posizione? Dovremmo forse accettare case diurne che sprofondano sotto la terra e viceversa?
2. Riferendoci all'esempio retoriano, com'è possibile che le 6 ore diurne antimeridiane possano avere una durata così diversa da quelle diurne pomeridiane?
A parte le fantasticherie di chi ancora crede – fornendo come prova l'incomprensione dei testi – ad una fantomatica suddivisione del cielo in settori uguali, un assurdo astronomico e di conseguenza anche astrologico, il vero problema, di cui gli astrologi greci erano ben consapevoli, sta nella suddivisione dell'emisfero diurno o notturno in 3 + 3 sezioni, ciascuna di due ore temporal-locali, ossia ineguali financo tra loro. Ed è solo risolvendo questo problema che si possono collocare i corpi celesti in una casa piuttosto che in un'altra.[27] Di qui, forse, la moltiplicazione e la grande diffusione delle sorti, che consentono di svicolare dalle case...
Ne riparleremo a suo luogo... si Deus vult.

NOTE.

[1] Una traduzione seguita da commento si trova in O. Neugebauer & H. B. van Hoesen, Greek Horoscopes, Philadelphia 1959, p. 138 ss., citato nel seguito con la sigla GH. Una seconda traduzione è data in Rhetorius The Egyptian, Astrological Compendium, by James H. Holden, Tempe (AFA, Inc.) 42009, App. IV., p 211 ss., citato nel seguito con la sigla AC.

[2] Il testo del capitoletto ci è giunto in pessime condizioni, poiché è stato sicuramente ritagliato e riassemblato da uno o più copisti più o meno distratti e/o più o meno competenti. La prova evidente è data dall'esempio iniziale, che non è preceduto da alcuna introduzione. Tuttavia, la frase che introduce la seconda parte (cf. loc. cit. p. 223,13: Ἀλλὰ δεῖ τὸν τόπον ἀκριβεστέρως ἐκτίθεσθαι, ma occorre evidenziare il luogo con maggior precisione), anch'essa corrotta, doveva far parte dell'introduzione premessa all'esempio, nella quale verosimilmente si parlava della domificazione in uso, ma imprecisa; di qui, la necessità di illustrare le operazioni di calcolo in modo più preciso (ἀκριβεστέρως, avverbio comparativo rarissimo). Ciò nonostante, i dati consentono di ricostruire l'intera procedura di calcolo senza difficoltà.

[3] Per 'scientista' intendiamo quello studioso che in base a ragionamenti a tratti schizoidi confonde la realtà con le sue opinioni, che egli pretende d'imporre come verità rivelata. Lo scientismo è un virus culturale importato in Europa dall'occidente, la cui diffusione ha ormai raggiunto il livello di una pandemia irreversibile, mortale per la conoscenza.

[4] Gli editori pongono qui una lacuna, poiché la frase è monca. Noi, giusto per completare il senso ed utilizzando le parole di Tolemeo, integriamo con αὐτοῦ τοῦ ὁρίζοντος περιλαμβάνονται, ma potrebbe bastare anche il semplice λαμβάνονται.

[5] Va sottolineato che gli astrologi ellenistici chiamano 'centri' quei punti che, seguendo l'errato uso di Manilio e di Firmico, saranno poi chiamati 'cardini'. Riprenderemo l'argomento in un prossimo articolo.

[6] Secondo AC «the Greek text has 17°42'», ma il testo greco ha ιζ΄ μδ΄, cioè 17°44'.

[7] La lacuna nel testo è palese, e va integrata con le stesse parole di Retorio: αὗται δὲ μοῖραι ἔσονται ἀρχαὶ τοῦ ιβ΄ τόπου.

[8] La formula per calcolare l'α di un punto dell'eclittica è: tan(α) = cos(ε)*tan(λ). In Excel tale formula si scrive come segue: ARCTAN(COS(ε*PI.GRECO()/180)*TAN(λ*PI.GRECO()/180))*180/PI.GRECO(), ove ε è l'in­cli­na­­zione dell'eclittica e λ la longitudine eclittica.

[9] Purtroppo la splendida (faciles a parte) edizione critica del Piccolo commentario edita da A. Tihon (Le “petit commentaire” de Théon d'Alexandrie aux tables faciles de Ptolémée, Città del Vaticano [Bibl. Apostol. Vatic.] 1978) non pubblica questa tavola, che invece si trova nell'edizione dell'abate N. Halma (1822).

[10] Per l'ascensione obliqua utilizziamo la sigla αφ per significare che si tratta dell'ascensione retta (α) sotto una determinata latitudine geografica (φ).

[11] Non 137°42' come riporta AC.

[12] La frase tra le doppie parentesi quadre va espunta, poiché è una chiara glossa, per di più errata. GH traduce solo la nota sulla Luna, che a nostro parere è fuori luogo.

[13] Abbiamo già visto che i tempi ascensionali di 20°16' Toro sono 137°44', quelli di 29°7' Capricorno sono 31°20'; sottraendo il secondo al primo troviamo 106°24'.

[14] Cioè 211°20'(29”), che sono i tempi ascensionali di 29°7' Cancro, meno 137°44' = 73°36'.

[15] Il testo dice 6°16', errore di cui l'editore non s'è accorto.

[16] Il testo ha 16°46' in netto contrasto con i seguenti 13°48', che sono un errore in luogo di 13° 42' risultanti dall'interpolazione.

[17] Nel testo sono qui errati entrambi i valori: infatti, come risultato dà 16°46' Sagittario, mentre come inizio dell'VIII luogo dà 13°48', comunque errato, ancorché più vicino al risultato corretto. Ciò conferma i pasticci operati dai copisti (v. n. 2).

[18] In GH (p. 139, seconda colonna) si afferma che «two combined effects explain the difference. First, Rhetorius' longitude for M is not correct and should be 2;47, thus M - 5 = Capr. 27°47'. Secondly, if M is the culminating point to H, then M - 5° is in general not the culminating point to H - 5°. Indeed, using Theon's tables one finds that 29;4 culminates with 20:16 rising, thus a deviation of only 0;3°, caused by the rounding-off of the numbers in the tables». Innanzi tutto, se abbasso di 1° la longitudine del MC saltano tutti gli altri dati: l'ascendente, ad es., si abbasserebbe a 18°15' Toro. In secondo luogo, è puerile sottolineare che a 5° sottratti al MC non possano corrispondere 5° tolti all'ascendente. Infine, se nella Tavola di Teone (v. supra) si riportano 29°4' Capricorno, non si trovano affatto 20°16' Toro all'ascendente, bensì per interpolazione 31°17'(12”), che sono nel V clima l'ascensione obliqua di 20°19'(15”) Toro. Ci chiediamo se qualcuno si è accorto che, ricercando nella Tavola delle ascensioni sulla sfera retta il grado eclittico del suo MC, troverà, quale che sia la latitudine, l'ascensione obliqua del suo ascendente!

[19] Un'esauriente esposizione si trova in Al-Battani (sec. IX), cf. Al-Battano sive Albatenii Opus Astronomicum, Latine versum, adnotationibus instructum a C. Alph. Nallino, Mediolani (Hoepli) 1903, p. 73 s., una eccellente edizione da portare ad esempio a tutti gli editori in generale, ma soprattutto agli assiriologi, agli islamisti ed ai grecisti moderni. Una vera ed utile edizione critica, oltre ad un'adeguata descrizione in latino dei principi filologici seguiti ed un apparato critico, dovrebbe contenere una chiara traduzione, ovviamente sempre in latino, la quale costringerebbe l'editore ad precisare la sua interpretazione senza perdersi in fatue prolissità. Non è raro, infatti, il caso in cui il lettore si domandi che cosa l'editore abbia capito. Le inutili riedizioni sarebbero rarissime e le esondanti ed ingombranti bibliografie ridotte all'essenziale.

[20] Il verbo "subtract" nel greco è assente; “the ideal and fixed zodiac which...” dà a "fixed" una posizione attributiva che in greco non ha; κινούμεναι non può significare "variable" (in tal caso si direbbe μεταβάλλουσαι), bensì 'che sono in movimento'. Questo zodiaco ideale e fisso servirebbe come base per il calcolo degli aspetti: ai traduttori è sfuggito il significato di σχηματίζω, usato di norma al medio, ma qui nella rarissima forma attiva. Non solo: i gradi "ideal" sarebbero quelli che “always accurately make 30 degrees together”, e che cosa significa? È palese che il testo non è stato compreso.

[21] Cf. Eus. praep. ev. 6,2,78; Orig. Comm. in Gen., in Migne, PG XII 80,24.

[22] Sul significato del verbo νοέω, v. il nostro articolo Aristotele spiega l'aspetto verbale del presente e del perfetto. Il significato astrologico di ?????? ha verosimilmente messo in difficoltà i traduttori, i quali ricorrono al lessico filosofico ('intelligibile') o fantasioso ('ideale'), senza chiarirne il significato. Il solo che abbia cercato di capirne il senso è Cl. Saumaise, senza però risultati convincenti (cf. Cl. Salmasii, De annis climactericis et antiqua astrologia diatribae, Lugduni Batavorum 1648, pp. xxviii ss. della Praefatio).

[23] Il significato astrologico di νοητός ha verosimilmente messo in difficoltà i traduttori, i quali ricorrono al lessico filosofico ('intelligibile') o fantasioso ('ideale'), senza chiarirne il significato. Il solo che abbia cercato di capirne il senso è Cl. Saumaise, senza però risultati convincenti (cf. Cl. Salmasii, De annis climactericis et antiqua astrologia diatribae, Lugduni Batavorum 1648, pp. XXVIII ss. della Praefatio).

[24] Hdt. 2,109. Qualche scientista, contraddetto nelle sue convinzioni da questa testimonianza erodotea, in omaggio ai principi cui s'ispira la sua setta, ha proposto l'espunzione della frase! Una dettagliatissima disamina del luogo erodoteo si trova in K. Schaldach, Die antiken Sonnenuhren Griechenlands, Frankfurt a. M. (H. Deutsch) 2006, pp. 3 ss.

[25] Cf. Fr. Rochberg-Halton, Babylonian Seasonal Hours, in “Centaurus” 1989, pp. 146÷170, che riprende un precedente articolo di D. Pingree & E. Reiner, A Neo-Babylonian Report on Seasonal Hours, in “AOF” xxv (1974/1977) pp. 50÷55.

[26] Delle circa 100.000 tavolette in scrittura cuneiforme, la maggior parte delle quali trafugate ai legittimi proprietari, ad oggi ne è stata pubblicata una piccolissima parte. Finché non saranno tutte pubblicate, le certezze ostentate dagli storici dell'astronomia e dagli assiriologi, vanno considerate con estrema cautela, soprattutto perché assiriologi competenti, come lo fu il nostro Giovanni Pettinato, sono ormai mosche bianche. Gli studiosi sicentisti di nuova generazione più che a leggere e pubblicarte le tavolette trafugate, pensano a rieditare testi già editi... Qualche sospetto sulla competenza pare del tutto legittimo.

[27] Nel capitolo 14, che s'intitola Come si debbano trovare le 6 ore che distanziano l'oroscopo nei due sensi sia dal meridiano sia dal tramontante (cf. CCAG VIII,1, p. 223÷226), non tradotto in AC, Retorio spiega come calcolare la distanza oraria di un punto dell'eclittica (nell'esempio, quella di Saturno) per stabilire in qual luogo esso si trovi. Qui Retorio elude la norma tolemaica dei 5°! Il testo greco contiene banali errori di trascrizione, che hanno compromesso la comprensione degli editori.


[Dorno, 27 agosto 2024]


© Franco Luigi Viero

INDIETRO