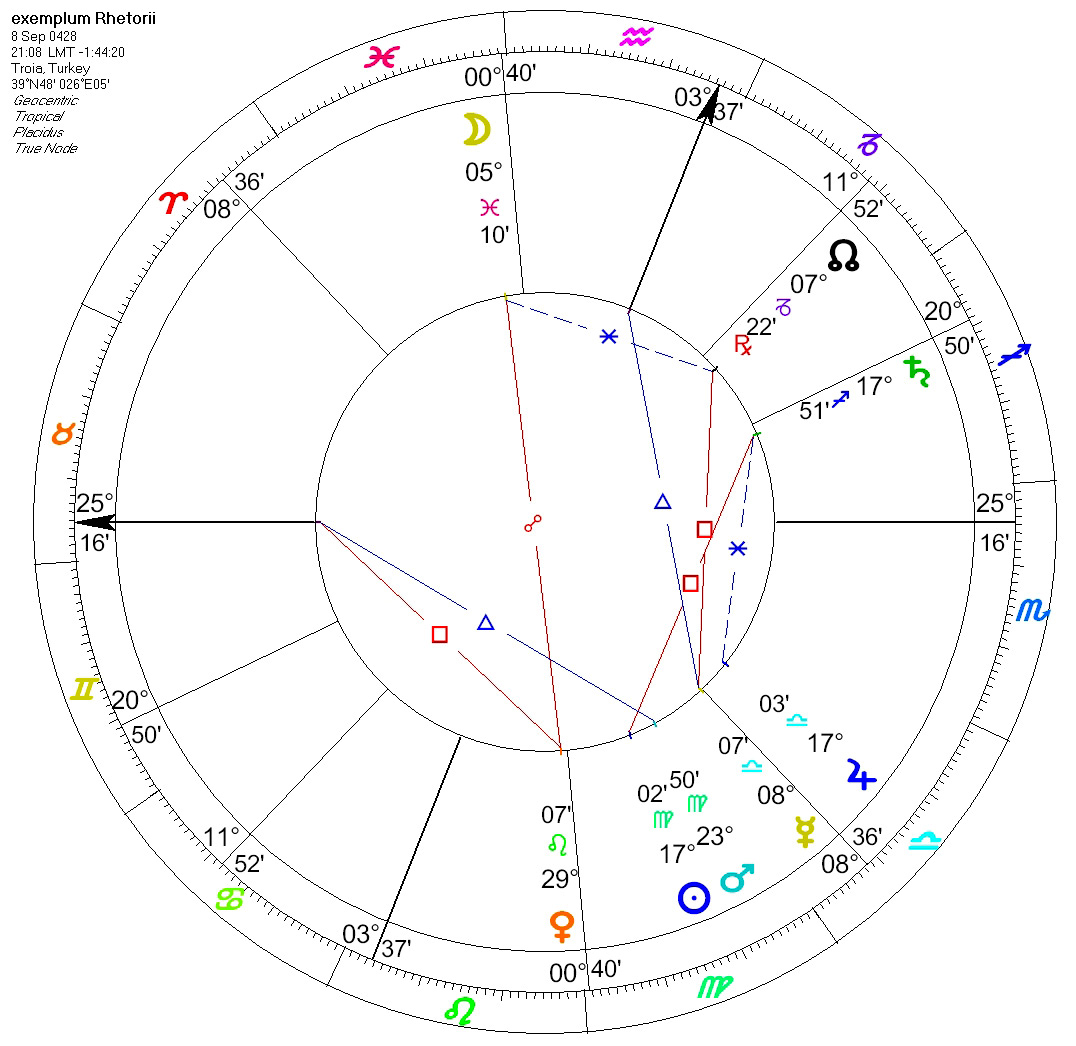
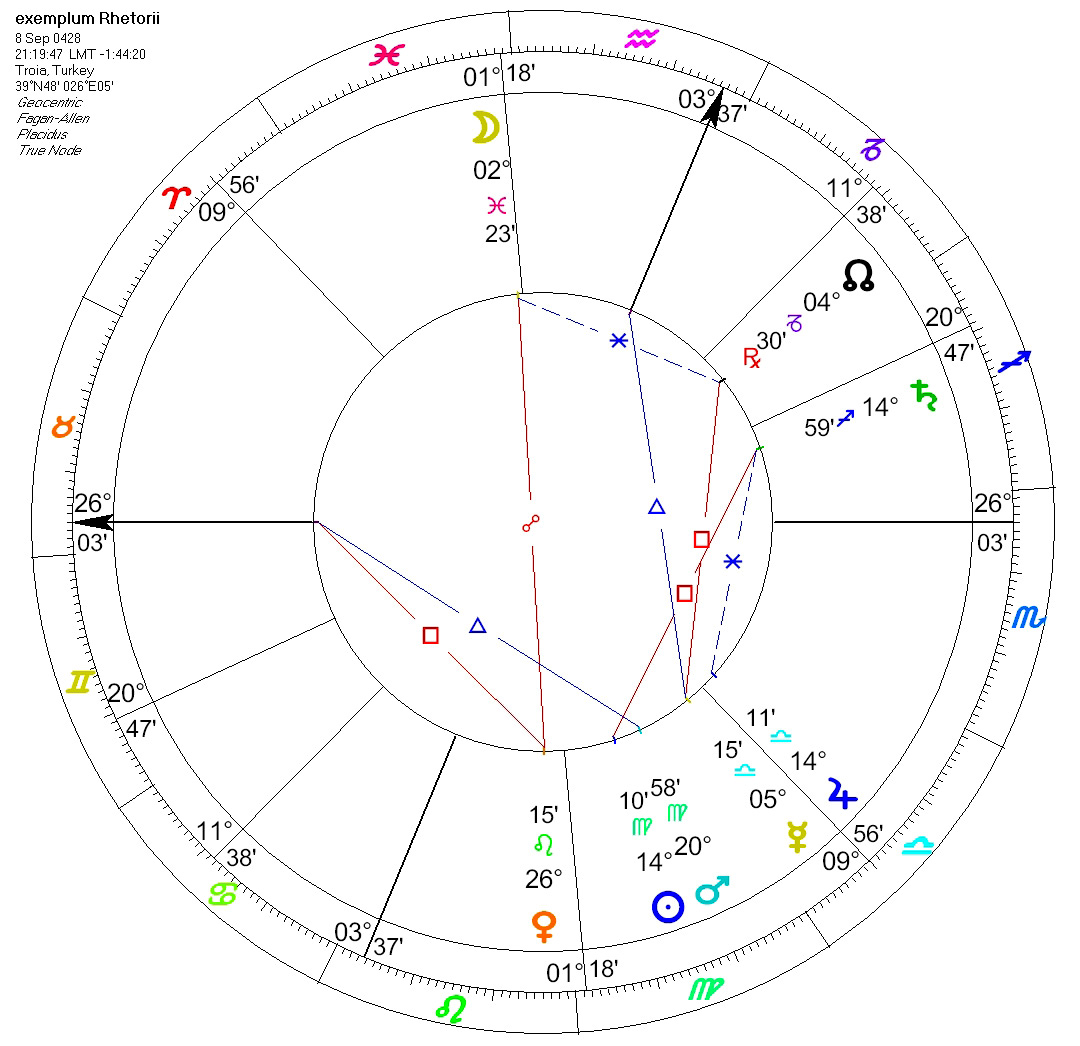
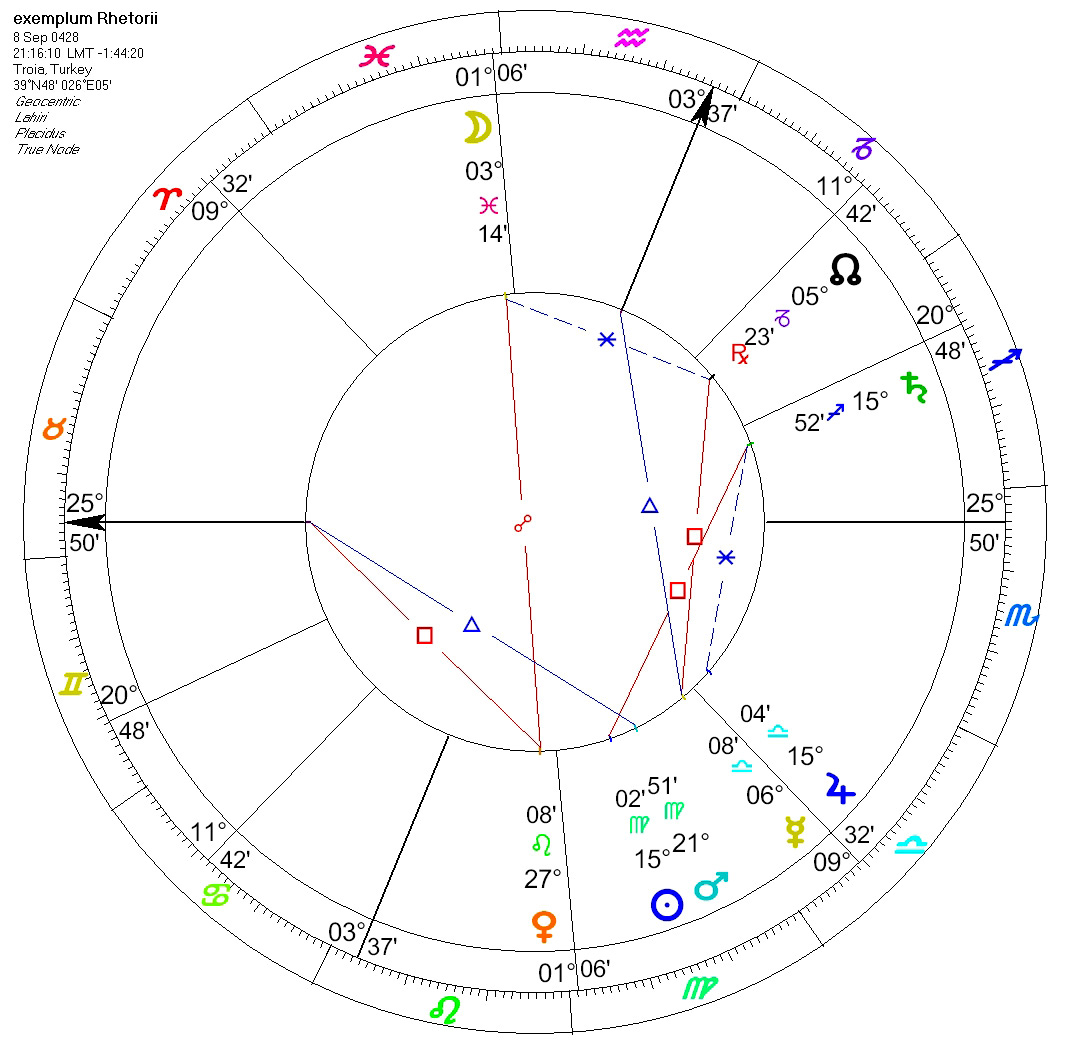
The house-division according to Rhetorius.


HAVING set our mind on an exhaustive exposition of the systems used by Hellenistic astrologers to divide the local sky into houses, but not wishing to overburden the content, we will here treat separately the system of domification expounded by Rhetorius. The Greek text, of which we propose the translation, is published in Catalogus codicum astrologorum Graecorum, vol. VIII.1, p. 221. The chapter is entitled “How one must (proceed to) find by degree (μοιρικῶς) the kentra of the twelve loci.”[1] Rhetorius begins by reporting the data:[2]

An example of a geniture: fifth clime, year of Diocletian 145, Thoth the 10th to 11th, beginning of the 4th hour of the night; the Sun (was in) 14°19' Virgo, the Moon 3° 4' Pisces, Saturn 14°31' Sagittarius, Jupiter 15°41' Libra, Mars 21°6' Virgo, Venus 25°40' Leo, Mercury 3°37' Libra, Horoscopus 25° 16' Taurus, Midheaven 3° 37' Water-pourer, ascending node 30°41' Capricorn, (preceding) conjunction 1°26' Virgo, the (Lot of) Fortune 6°31' Sagittarius, (that of) Daimon 14°1' Scorpio.

The Gregorian date is September 8, 428. In order to offer our reader the image of the sky of the Rhetorian example, we set in S(olar)F(ire) a locality of the 5th clime, ex. gr. Troy, in Turkey, with the following coordinates: 39°N48' and 26°E05', at 21h08m, local time (LMT): an almost obligatory choice, in order to make the Midheaven and the Ascendant coincide with those given by Rhetorius (see above, the chart on the left). Then we produced a second chart, changing the zodiac, from tropical to sidereal (Fagan-Allen), and a third one, changing the sidereal zodiac again, from Fagan-Allen to Lahiri, so that the Midheaven and Ascendant remained in their place: for the sidereal zodiac according to Fagan-Allen we had to change the time (21h19m47s) and the latitude (38°N47'), as well as for the zodiac according to Lahiri (21h16m10s and 39°N05'). 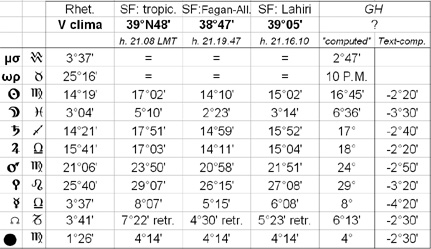In the table on the right, we see the differences: in the last two columns we show the data calculated by GH with the relative deviations given by the authors, while in the first column, corresponding to the symbols on the right, we display Rhetorius' data, in the second those given by SF for the tropical zodiac, in the third those according to the Fagan-Allen sidereal zodiac, and in the fourth those according to Lahiri. The domification is by Placidus. One will immediately notice that there is a considerable discrepancy between Rhetorius' positions and those of the tropical zodiac, which in some cases become negligible if the comparison is made with the two sidereal zodiacs. Yet, Rhetorius clearly states that he used the sidereal zodiac, not the tropical one. Hence, one naturally wonders why GH compares data that are not comparable. Indeed, it is known that O. Neugebauer despised astrology, good follower of scientism as he was;[3] however, one may suspect that both he and his colleague van Hoesen did not understand the text (see below). It goes without saying that in the following the operations performed by Rhetorius will be checked using the latitude of 40°N56', 5th clime, and 23°51'20” for the inclination of the ecliptic, both taken from Ptolemy. Let us begin reading again:

We shall explain (how to find) the degrees (of each) of the twelve loci in order to show according to the natural and logical calculation the distances in degrees of the central and declining loci in the following way.
Since <we take> the 5 degrees pre-ascending <the horizon>,[4] as Ptolemy says, subtracting those from the given rising degree, we will find for the origin of the centrality[5] of the horoscope 20°16' (Taurus); to these degrees correspond, in the sphaera recta, ascending times equal to 137° 44'. Taking the hourly times of 20°16' Taurus in the fifth clime, that is 17°44',[6] and doubling them, we will obtain hourly times equal to 35°28'; subtracting them from 137°44' we will find a remainder of 102°16'; (well,) together with these 102°16' culminate at sphaera recta 13°21' Aries. <And these degrees will be the beginning of the 12th locus>.[7]

We must pause to explain what ascensions in the sphaera recta are. Ptolemy discusses this topic in the last chapter of Book I of the Almagest (p. 47). If we rotate the local sphere until the equator coincides with any meridian, we will obtain the sphaera recta, so defined because equator and horizon, which in this case passes through the poles, cut each other at right angles and the observer's latitude is 0°. In these conditions any segment of the ecliptic will rise on the horizon in exactly the same times as the corresponding segment of right ascension (α). If, for example, we take on the ecliptic the 30° of Aries, in the sphaera recta they will ascend in the same times corresponding to the right ascension of the first 30° of the ecliptic.[8] Proceeding by means of the formula to calculate the α of 30° Aries, we will obtain 27°50', which are the same ascensional times indicated by Ptolemy. The ascensional times, however, precisely because they are ascensions, are presumed to arise on the horizon of a place, whatever it may be.
Theon of Alexandria in his Abridged Commentary on the Ptolemaic Tables for Ready Use[9] provides a "Table of Ascensions in the Right Sphere" for each degree of the Zodiac at any latitude. This table presupposes that the observer is at noon, that is, with the Sun at the zenith, of any place. It is known that the latitude of Midheaven (MC) is always 0° and that the oblique ascension of the horoscope is given by the α of MC + 90°. If, therefore, 90° are added to the α of a point of the ecliptic at noon, the oblique ascension (αφ) of the horoscope will be obtained.[10] But in the sphaera recta there is no oblique ascension or ascensional difference, so this sum will give the α of the horoscope, to which—consulting the tables—a precise point of the ecliptic will correspond.
Well, what does Rhetorius do? He has already found the ascendant degree (25°16' Taurus), but, wanting to follow Ptolemy according to whom the first house begins five degrees backwards, he subtracts 5°: thus, 25°16' Taurus – 5° = 20°16'. He then looks in the “Table of Ascensions in the Right Sphere” for the ascending times corresponding to 20°16' Taurus. Below, we propose that Table calculated by Excel: the values in brown show the sexagesimal degrees, the ones below in black show the corresponding decimals. In the first column are listed the ecliptic degrees assumed at midheaven, i.e. at noon; on the same line are given the ascensions for each sign.


By interpolating between 20° (137°27'51”) and 21° Taurus (138°28'39”) we find that 20°16' Taurus corresponds to 137°44'(03”), which are the same ascensional times given by Rhetorius.[11] It is now necessary to find the hourly times corresponding to 20°16' Taurus in the 5th clime. Contrary to what GH states, Theon does not give the hourly times for each degree, but only the ascensional ones. So let us take the Ptolemaic “Table of ascensions”, 5th clime, and, by interpolating between 31°05' (20° Taurus) and 38°51' (30° Taurus), we will find that the ascensional times of 20°16' Taurus correspond to 31°18' (to be exact 31°17'26”). Subtracting 31°18' from the α of 20°16' (i.e. 47°44'26”), we get the ascensional difference (16°27'); adding 1/6 of this ascensional diff. to 15°, we will obtain the hourly times of 20°16' Taurus, i.e. 17°44'30”, which Rhetorius rounds to 17°44'.
Since each house is 2 hours away from the other, Rhetorius doubles the temporal hour (17°44' × 2) and subtracts 35°28' from 137°44'; then he enters the result of 102°16' in the “Table of Ascensions on the Right Sphere” to find out which degree of the ecliptic it corresponds to: he says 13°21' Aries, even if in reality the interpolation gives 13°14' (40"), which is the point where the 12th locus begins. But let us proceed:

And again in the same order, subtracting from 102°16' (the same) 35°28', we will find a remainder of 66°48', together with which we will find that, always in the sphaera recta, 4°8' Pisces culminate. These 4°8' Pisces will be for us the origin of the eleventh place, [[while 3°11' of the Water-pourer (will be) the origin of the tenth, so that the Moon is rather in the tenth place]].[12] Again, subtracting 35°28' from 66°48' (we will have) a remainder of 31°20', together with which we will find that 29°7' Capricorn culminate. These will be the origin of the midheaven. At the beginning, however, the midheaven was at 3°37' Water-pourer; therefore (the origin) precedes by 4°30'; but it should have been 5°. Anyhow, it differs by a trifle, by 30'.

Some interpolations are not very precise: to the α of (66°48' – 90° =) 336°48' correspond 4°53'(26”) Pisces, not 4°8'. Better is the one for the 10th house: in fact, together with (66°48' – 35°28' =) 31°20', that is (31°20 – 90° =) 301°20', 29°6'32” Capricorn culminate. Here Rhetorius gives an interesting explanation as to why such a small difference occurred, but more on this below.
The astrologer then goes on to subdivide the loci in the west quadrant:

Starting all over again (πάλιν), since from 29°7' Capricorn to 29°7' Cancer the times of the culminations of the hemisphere are 180°, of which the simultaneous culminations from 29°7' Capricorn to 20°16' Taurus are six times 17° 44', i.e. 106° 24',[13] it follows that the simultaneous culminations from 20°16' Taurus to 29°7' Cancer are equal to the times missing for the supplement of the hemisphere, (i.e.) 73°36'.[14] One third of these is 24°32' times. Subtracting 24°32' from the given degrees, 31°20', there remain 6°48', together with which culminate 6°13' Capricorn; thus 6°13' Capricorn will be the beginning of the ninth locus.[15] Again, from 6°48' subtracted 24°32', there remain 342°16', together with which culminate 13°42' Sagittarius;[16] therefore 13°42' Sagittarius will be the beginning of the 8th locus.[17] Again, taking away 24°32' from 342°16', there remain 317°44', together with which culminate 20°16' Scorpio, which is the opposite point to the horoscope. The diametrical points to those will be the beginnings of the subterranean loci, that is, the 2nd, 3rd, 4th, 5th, 6th.

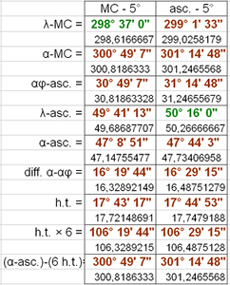That is how the house-division according to Rhetorius ends. In order to find where the error that generated the aforementioned 30' discrepancy lurks, let us redo the calculations using the trigonometric formulae, keeping ε = 23°51'20” and φ = 40°56' (5th clime). In the table on the left, first column, we show the data obtained starting from the ecliptic longitude of the MC (in green); in the second column, the same data obtained starting from the ecliptic longitude of the Ascendant. It will be noted that the MC in 28° 37' Capricorn places the Ascendant in 19°41' Taurus, while the Ascendant in 20°16' Taurus places the MC in 29°02' Capricorn. In other words, these two data cannot coexist. The reasons given by GH have no merit.[18]. But a careful reader might ask: how come in the three sky charts shown above Ascendant and MC correspond to those given by Rhetorius? The answer is simple: because, as stated above, both the geographical latitude and the time have been slightly changed.
To summarise, the elaborate system set out by Rhetorius comes down to a few simple steps:
1. Having found the Ascendant and the MC, one deducts 5° from the former;
2. Once the α of the Ascendant is calculated, its semi-arc is computed, which is really the distance in α between the Ascendant itself and the MC;
3. Once the semi-arc has been divided by 3, the corresponding points on the ecliptic will be the beginnings of the houses contained in the quadrant; and each section of a third equals twice the temporal-local time of the Ascendant.
This system would become famous as “domification of Alcabitius” (10th century), which we will come back to in another article.[19]
Now let us take up Rheorius'explanation of the 30' discrepancy, i.e. 4°30' instead of 5°:

Such is the cause. Ptolemy says that neither the temporal nor the local degrees should precede the centre, but those of the noetic zodiac (should, a zodiac) which does not move (τοῦ ἀκινήτου) recreating the local and temporal degrees (after the style of those) in motion (τοῦ σχηματίζοντος τὰς κινουμένας τοπικάς τε καὶ χρονικὰς μοίρας). We, on the other hand, have assumed the 5 degrees in motion and sensitive. When, therefore, Ptolemy says “the right-hand (places) hexagons in regard to these 30 degrees (τοὺς ταύταις ταῖς λ΄μοίραις δεξιοὺς ἑξαγώνους)", he is speaking of the noetic ones, which in fact shape one another (σχηματίζουσαι ἀλλήλας) every 30° with precision, while those in motion are detected in a rough way.

It should be noted immediately that the quotation is incorrect, since Ptolemy says “the right-hand hexagonal degrees to these 30 degrees (τὰς ταύταις ταῖς λ΄μοίραις δεξιὰς ἑξαγώνους)". The use of the masculine (τοὺς) instead of the feminine (τὰς) twists the meaning and forces the reader to think of places instead of degrees. It is also possible that an ignorant copyist, reading ἑξαγώνους, which applies to both the masculine and the feminine, altered the text.
Now let us compare GH's translation: "Ptolemy says neither that one must subtract from the center time degrees nor (that one must subtract) longitudinal degrees, but the (degrees) of the ideal and fixed zodiac which (is the basis of the calculation) of the aspects, (i.e.) the variable longitudinal and time degree. We, however, took the variable and perceptible 5 degrees. Thus, when Ptolemy says “and the sextile which is to the right of these 30 degrees,” then he is speaking of the ideal (degrees), for these are (degrees) which always accurately make 30 degrees together; but the variable (degrees) give only an approximate (total)."
In this translation, the authors seem to have made a bit of a mess.[20] The first question to ask is: what is this noetic zodiac (ὁ νοητὸς ζωδιακός), translated by GH as 'ideal'?
A passage of Origen—quoted by Eusebius—is just what we need:[21]

Φέρεται δὴ θεώρημα ἀποδεικνύον τὸν ζωδιακὸν κύκλον ὁμοίως τοῖς πλανωμένοις φέρεσθαι ἀπὸ δυσμῶν ἐπὶ ἀνατολὰς δι ἑκατὸν ἐτῶν μοῖραν μίαν, καὶ τοῦτο τῷ πολλῷ χρόνῳ ἐναλλάττειν τὴν θέσιν τῶν δωδεκατημορίων· ἑτέρου μὲν τυγχάνοντος τοῦ νοητοῦ δωδεκατημορίου, ἑτέρου δὲ τοῦ ὡσανεὶ μορφώματος· τὰ δὲ ἀποτελέσματά φασιν εὑρίσκεσθαι οὐκ ἐκ τοῦ μορφώματος, ἀλλ' ἐκ τοῦ νοητοῦ ζωδίου· ὅπερ οὐ πάνυ τι δυνατὸν καταλαμβάνεσθαι.

It is well known the theorem according to which it is shown that the zodiacal circle, as well as the wandering (stars), moves from west to east by one degree every hundred years, and this fact, as so long time goes by, changes the position between the (respective) dodecatemoria, so that one dodecatemorion results noetic, the other (corresponding to it) results from the figure. Yet they say that the events (to come) are drawn not from the figure, but from the noetic sign. This is truly inconceivable!

The zodiacal circle that moves one degree every hundred years is therefore the sidereal one, made up of figures visible with the physical eyes, while the other, the noetic one, i.e. seen with the eyes of the mind, does not move.[22] It should be remembered that according to the celestial mechanics described geometrically by Ptolemy, the earth does not move and the zodiac always starts from the spring equinox. Therefore, the noetic zodiac, which does not move, is the tropical one and follows the sidereal zodiac, while the zodiac that moves, which can be seen with the naked eye, is the sidereal one.[23] The most interesting and astrologically valuable observation is that future events are drawn—the Chaldeans presumably said—from the tropical zodiac, not the sidereal one!
According to the authors of GH “Rhetorius is surprised that etc.”. Indeed, Rhetorius does not show any surprise, but, in order to safeguard his professionalism—it is only our hypothesis—he calls into question the two zodiacs, the noetic, i.e. tropical, and the sidereal. That he used the sidereal positions of the wandering stars, we have already seen, but the discrepancy between the departing and the arriving midheaven has nothing to do with the two zodiacs.
The division of the day, from sunrise to sunset and from sunset to the next sunrise, into 6 + 6 double hours was already known to the Mesopotamian astrologers, i.e. the Chaldeans. Herodotus (5th century) was already aware of it: “The Greeks learnt the sundial, the gnomon and the twelve parts of the day from the Babylonians.”[24] In other words, the subdivision of the sky into twelve sections of two hours each was already applied by the Chaldeans: the name of this double hour was bēru.[25] Unfortunately, however, the information about the calculations was transmitted vaguely or inaccurately, or not at all; which led the Greek astronomers to rack their brains to find an acceptable solution.[26]
The ingenious use of ascensions in the sphaera recta, however, lays itself open to two objections:
1. At any latitude other than 0°, since the horizon no longer passes through the poles of the world, what happens to the sectors delimited by the circles of declination that on the right sphere coincide with the circles of position? Should we accept diurnal houses sinking below the earth and vice versa?
2. Referring back to the Rhetorian example, how is it possible that the 6 antemeridian diurnal hours can have such a different duration from the 6 afternoon diurnal hours?
Quite apart from the fantasies of those who still believe-giving as evidence their incomprehension of the texts-in a phantom subdivision of the sky into equal sectors, an astronomical and consequently also astrological absurdity, the real problem, of which the Greek astrologers were well aware, lies in the subdivision of the diurnal or nocturnal hemisphere into 3 + 3 sections, each of two temporal-local hours, i.e. unequal even to each other. And it is only by solving this problem that celestial bodies can be placed in one house rather than another.[27] Hence, perhaps, the multiplication and great diffusion of the lots, which allow one to dodge the houses...
We will talk about that in due course..., si Deus vult.

NOTES.

[1] A translation followed by a commentary is found in O. Neugebauer & H. B. van Hoesen, Greek Horoscopes, Philadelphia 1959, p. 138 ff., cited in the following as GH. A second translation is given in Rhetorius The Egyptian, Astrological Compendium, by James H. Holden, Tempe (AFA, Inc.) 42009, App. IV., p. 211 ff., cited below as AC.

[2] The text of the chapter has come down to us in very poor condition, as it was almost certainly cut out and reassembled by more or less inattentive and/or more or less competent copyists. Evidence of this is provided by the opening example, which is not preceded by any introduction. However, the sentence introducing the second part (cf. loc. cit. p. 223,13: Ἀλλὰ δεῖ τὸν τόπον ἀκριβεστέρως ἐκτίθεσθαι, “But the locus needs to be located more precisely”), also corrupted, must have been part of an introduction preceding the example, in which the domification in use was likely mentioned as imprecise; hence, the need to illustrate the calculating operations "more precisely" (ἀκριβεστέρως, a very rare comparative adverb). Nonetheless, the data allow the entire calculation procedure to be reconstructed without difficulty.

[3] By 'follower of scientism' we mean that scholar who on the basis of sometimes schizoid reasoning, confuses reality with his own opinions, which he claims to impose as irrefutable truth. Scientism is a cultural virus imported into Europe from the West, the spread of which has now reached the level of an irreversible pandemic, mortal to knowledge.

[4] The editors put a lacuna here, as the sentence is incomplete. We, just to complete the sense, using Ptolemy's words, integrate with αὐτοῦ τοῦ ὁρίζοντος περιλαμβάνονται, but the simple λαμβάνονται could also suffice.

[5] It should be stressed that Hellenistic astrologers called “centres” those points that, following the erroneous usage of Manilius and Firmicus, would later be called “pivots”. We will return to this topic in a future article.

[6] According to AC “the Greek text has 17°42'”, but the Greek text has ιζ΄ μδ΄, i.e. 17°44'.

[7] The lacuna in the text is obvious, and should be supplemented with Rhetorius' own words: αὗται δὲ μοῖραι ἔσονται ἀρχαὶ τοῦ ιβ΄ τόπου.

[8] The formula for calculating the α of an ecliptic point is: tan(α) = cos(ε)*tan(λ). In Excel (Italian version) this formula is written as follows: ARCTAN(COS(ε*PI.GRECO()/180)*TAN(λ*PI.GRECO()/180))*180/PI.GRECO(), where ε is the inclination of the ecliptic and λ is the ecliptic longitude.

[9] Unfortunately, the splendid (aside from faciles) critical edition of the “Abridged Commentary” edited by A. Tihon (Le “petit commentaire” de Théon d'Alexandrie aux tables faciles de Ptolémée, Città del Vaticano [Bibl. Apostol. Vatic.] 1978) does not publish this table, which is instead found in the edition of Abbot N. Halma (1822).

[10] For oblique ascension we use the letters αφ to signify that it is the right ascension (α) under a given geographical latitude (φ).

[11] Not 137°42' as AC writes.

[12] The words between the double square brackets should be expunged, as it is a clear gloss, moreover incorrect. GH only translates the note on the Moon, which in our opinion is misplaced.

[13] We have already seen that the ascending times of 20°16' Taurus are 137°44', those of 29°7' Capricorn are 31°20'; subtracting the latter from the former we find 106°24'.

[14] That is 211°20'(29”), which are the ascending times of 29°7' Cancer, minus 137°44' = 73°36'.

[15] The text says 6°16', an error the editor did not realise.

[16] The text has 16°46' in stark contrast to the following 13°48', which is an error instead of 13°42' resulting from interpolation.

[17] In the text, both values are wrong here: in fact, as a result it gives 16°46' Sagittarius, while as the beginning of the 8th locus it gives 13°48', still wrong, although closer to the correct result. This confirms the bungling done by the copyists (see note 2).

[18] In GH (p. 139, second column) it is stated that "two combined effects explain the difference. First, Rhetorius' longitude for M is not correct and should be 2;47, thus M - 5 = Capr. 27°47'. Secondly, if M is the culminating point to H, then M - 5° is in general not the culminating point to H - 5°. Indeed, using Theon's tables one finds that 29;4 culminates with 20:16 rising, thus a deviation of only 0;3°, caused by the rounding-off of the numbers in the tables." First of all, if one lowers the longitude of the MC by 1°, all other data alter: the Ascendant, for example, would lower to 18°15' Taurus. Secondly, it is puerile to point out that 5° subtracted from the MC cannot correspond to as many 5° removed from the Ascendant. Finally, if in Theon's Table (see above) you enter 29°4' Capricorn, you will not find 20°16' Taurus as Ascendant at all, but—by interpolation—31°17'(12”), which in the 5th clime correspond to the oblique ascension of 20°19'(15”) Taurus. Now, we wonder if anyone has noticed that, entering the ecliptic degree of his own MC in the “Table of Ascensions in the right sphere”, the figure by side, whatever the latitude, is the oblique ascension of his own Ascendant!

[19] A full exposition is found in Al-Battani (9th cent.), cf. Al-Battano sive Albatenii Opus Astronomicum, Latine versum, adnotationibus instructum a C. Alph. Nallino, Mediolani (Hoepli) 1903, p. 73 f., an excellent edition to be held up as an example to all editors in general, but especially to modern Assyriologists, Islamists and Greek scholars. A true and useful critical edition should contain, besides an adequate Latin exposition of the philological principles followed and a critical apparatus, a clear Latin translation together with a Latin commentary, which would force the editor to make clear his interpretation without getting lost in empty verbosity. Indeed, it is not uncommon for the reader to wonder what the editor has understood. Unnecessary re-editions would be extremely rare and the overflowing and cumbersome bibliographies reduced to the essential.

[20] The verb “to subtract” in the Greek text is absent; “the ideal and fixed zodiac which...” gives “fixed” an attributive position that it does not have in Greek; κινούμεναι cannot mean “variable” (in which case one would say μεταβάλλουσαι), but “which are in motion”. Such an ideal and fixed zodiac would serve as the basis for calculating aspects: the translators missed the meaning of σχηματίζω, normally used in the middle, but here in the very rare active form. Not only that: “ideal” degrees would be those that “always accurately make 30 degrees together”, and what does that mean? It is clear that the text has not been understood.

[21] Cf. Eus. praep. ev. 6,2,78; Orig. Comm. in Gen., in Migne, PG XII 80,24.

[22] On the meaning of the verb νοέω, see our article Aristotele spiega l'aspetto verbale del presente e del perfetto.

[23] The astrological meaning of νοητός has probably puzzled the translators, who have resorted to philosophical ('intelligible') or fanciful ('ideal') lexicon without clarifying the meaning. The only one who tried to understand the meaning was Cl. Saumaise, but without convincing results (cf. Cl. Salmasii, De annis climactericis et antiqua astrologia diatribae, Lugduni Batavorum 1648, pp. XXVIII ff. of the Praefatio).

[24] Hdt. 2,109. Some follower of scientism, contradicted in his convictions by this Herodotus' testimony, in homage to the principles that inspire his sect, has proposed the expunction of the phrase! A very detailed examination of the Herodotean passage can be found in K. Schaldach, Die antiken Sonnenuhren Griechenlands, Frankfurt a. M. (H. Deutsch) 2006, pp. 3 ff.

[25] Cf. Fr. Rochberg-Halton, Babylonian Seasonal Hours, in “Centaurus” 1989, pp. 146÷170, who draws on an earlier article by D. Pingree & E. Reiner, A Neo-Babylonian Report on Seasonal Hours, in “AOF” xxv (1974/1977) pp. 50÷55.

[26] Of the 100,000 tablets in cuneiform writing, most of which were stolen from their rightful owners, only a tiny fraction has been published to date. Until they are all published, the certainties flaunted by historians of astronomy and Assyriologists must be treated with extreme caution, especially because competent Assyriologists, such as our Giovanni Pettinato, are now terribly rare. The new generation of scholars, the most of whom infected by the virus of scientism, rather than reading and publishing the stolen tablets, think about re-editing texts already published... Some suspicions about competence seem quite legitimate.

[27] In chapter 14, which is entitled “How to find the 6 hours that distance the horoscope in both directions from both the meridian and the sunset” (cf. CCAG VIII.1, p. 223÷226), not translated by AC, Rhetorius explains how to calculate the hourly distance of a point on the ecliptic (in the example, that of Saturn) to establish where it is located. Here Rhetorius evades the Ptolemaic norm of 5°! The Greek text contains trivial transcription errors, which compromised the editors' understanding.


[Dorno, August 27, 2024]


© Franco Luigi Viero

INDIETRO